<<wstecz   SORTOWANIE

Ustawianie danych lub informacji według określonego kryterium, zwykle w kolejności rosnącej (tj. od najmniejszego elementu do największego) lub malejącej (odwrotnie). Uporządkowanie zbioru danych (np. bazy danych) lub informacji znacznie upraszcza i przyspiesza przeszukiwanie takich zbiorów. Czynność porządkowania jest jedną z najczęściej wykonywanych operacji w komputerze, często bez udziału użytkownika. Problem porządkowania jest jednym z najważniejszych problemów informatycznych. Opracowano dla niego wiele algorytmów, z których najpopularniejsze są przedstawione poniżej.

• Sotrowanie bąbelkowe (bubblesort)
• Sortowanie przez wstawianie (insertionsort)
• Sortowanie przez wymianę/wybór (selectionsort)
• Sortowanie szybkie (quicksort)
• Sortowanie stogowe (heapsort)
• Sortowanie przez zliczanie (countingsort)
• Sortowanie przez scalanie (mergesort)
• koszykowe

Sotrowanie bąbelkowe (bubblesort)

Jedną z prostszych metod jest sortowanie bąbelkowe, polegające na przestawianiu sąsiadujących ze sobą niekolejnych elementów zbioru. Na skutek jego działania elementy o większych wartościach są wynoszone jak bąbelki w podgrzewanej wodzie. Przedstawmy to na przykładzie, gdzie zamiany realizowane będą od lewej (dół) do prawej (góra).

Jak można zauważyć z tabeli, algorytm bąbelkowy wynosi najpierw elementy o największej wartości. Można się także spodziewać, że nie zawsze będzie konieczne porównywanie każdego elementu z każdym.


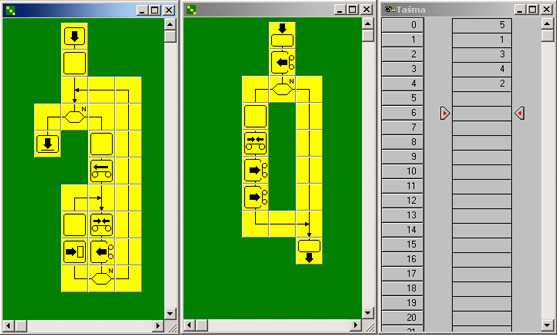
Algorytm sortuje liczby na taśmie. Sprawdzenie, czy jest konieczne przestawienie liczb w tablicy, realizowane w procedurze Przestaw (osobna plansza). W wypadku wystapienia takiej sytuacji, procedura dokonuje zamiany miejsc liczb na taśmie. Do poprawnego działania algorytmu trzeba mieć otwarte okno taśmy z wprowadzonymi danymi.

Sortowanie przez wstawianie (insertionsort)

Zasada działania tego algorytmu jest często porównywana do porządkowania kart w wachlarz podczas gry. Każdą kartę wstawiamy w odpowiednie miejsce, tzn. po młodszej, ale przed starszą. Podobnie jest z liczbami.
Pierwszy element pozostaje na swoim miejscu. Następnie bierzemy drugi i sprawdzamy, w jakiej relacji jest on z pierwszym. Jeśli jest niemniejszy, to zostaje na drugim miejscu, w przeciwnym wypadku wędruje na pierwsze miejsce. Dalej sprawdzamy trzeci element (porównujemy go do dwóch pierwszych i wstawiamy w odpowiednie miejsce), czwarty (porównujemy z trzema pierwszymi), piąty itd. Idea działania algorytmu opiera się na podziale ciągu na dwie części: pierwsza jest posortowana, druga jeszcze nie. Wybieramy kolejną liczbę z drugiej części i wstawiamy ją do pierwszej. Ponieważ jest ona posortowana, to szukamy dla naszej liczby takiego miejsca, aby liczba na lewo była niewiększa a liczba na prawo niemniejsza. Wstawienie liczby do posortowanej tblicy wyaga więc czasu O(n). Wynika z tego złożoność algorytmu: O(n2)
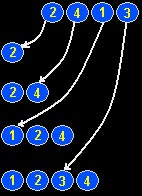
Oto przykład dla nieposortowanego ciągu <2, 4, 1, 3>

Sortowanie przez wymianę/wybór (selectionsort)

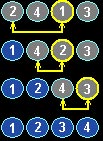
Metoda ta nazywana jest sortowaniem przez wymianę gdyż na początku szukany jest najmniejszy element, po znalezieniu go jest on zamieniany z pierwszym elementem tablicy.
Następnie szukany jest znów najmniejszy element, ale począwszy od elementu drugiego (pierwszy - najmniejszy jest już wstawiony na odpowiednie miejsce), po jego znalezieniu jest on zamieniany z drugim elementem. Czynność tą powtarzamy kolejno na elementach od trzeciego, czwartego, aż do n-tego.

Sortowanie szybkie (quicksort)

Algorytm sorotwania szybkiego jest uważany za najszybszy algorytm dla danych losowych.
Zasada jego działania opiera się o metodę dziel i zwyciężaj. Zbiór danych zostaje podzielony na dwa podzbiory i każdy z nich jest sortowany niezależnie od drugiego.
Dla zadanej tablicy a[l..p] wybieramy element v=a[l] i przeszukujemy resztę tablicy (tzn. a[l+1..p]) tak długo, aż nie znajdziemy elementu większego niż a[l]. Następnie przeszukujemy tą tablicę od strony prawej póki nie znajdziemy elementu nie większego niż a[l]. Gdy to osiągniemy, zamieniamy miejscami te dwa elementy i zaczynamy cały proces od początku. Algorytm działa tak długo, aż wskaźnik poruszający się w lewo i wskaźnik poruszający się w prawo spotkają się. Należy wówczas zamienić element v=a[l] z ostatnim elementem lewej części tablicy.
Mimo, że w najgorszym przypadku algorytm ma złożoność kwadratową, jest on bardzo często stosowany. Powodem tego jest niska- liniowologarytmiczna, złożoność w średnim przypadku.

Sortowanie stogowe (heapsort)

Jest to metoda bardziej skomplikowana niż sortowanie bąbelkowe czy przez wstawianie, ale za to działa w krótszym czasie. Zrozumienie algorytmu HeapSort wymaga zaznajomienia się z pojęciem Kopca/Stogu. Budowa drzewa binarnego z elementów tablicy, którą mamy posortować wygląda następująco:

• Zaczynamy od pierwszego elementu tablicy, który będzie korzeniem
• Każdy następny i-ty element tablicy będzie miał co najwyżej dwa następniki o wyrazach odpowiednio: 2*i oraz 2*i+1
• Łatwo stwierdzić, że dla każdego i-tego elementu (oprócz korzenia) numer elementu w tablicy, będącego jego poprzednikiem określa się wzorem: i div 2

Po zbudowaniu drzewa należy wykonać odpowiednie instrukcje, które zapewnią mu warunek kopca. Należy więc sprawdzać (poczynając od poprzednika ostatniego liścia schodząc w górę do korzenia) czy poprzednik jest mniejszy od następnika i jeżeli tak jest to zamienić je miejscami. Po wykonaniu tych czynności drzewo binarne zamieniło się w stóg. Z jego własności wynika, że w korzeniu znajduje się największy element. Korzystając z tego faktu możemy go pobrać na koniec tablicy wynikowej a na jego miejsce wstawić ostatni liść. Po pobraniu korzenia tablica źródłowa zmniejszyła się o 1 element a porządek kopca został zaburzony (nie wiadomo, czy ostatni liść będący teraz korzeniem jest rzeczywiście największym elementem). By przywrócić warunek stogu należy ponownie uporządkować jego elementy, tym razem jednak zaczynając od korzenia (ponieważ to on jest nowym elementem). Po przywróceniu porządku w kopcu możemy znów pobrać korzeń i wstawić go do tablicy wynikowej (tym razem na drugie miejsce od końca), wstawić na jego miejsce liść i zmniejszyć rozmiar tablicy źródłowej o 1. Tu pętla się zamyka. Wykonujemy te czynności aż do ostatniego korzenia. Po całkowitym wyczyszczeniu kopca w tablicy wynikowej będziemy mieli posortowane elementy z tablicy wejściowej. Aby zlikwidować drugą tablicę (co zwiększa złożoność pamięciową algorytmy) wystarczy w kolejnych krokach odkładać korzenie w tej samej tablicy, od końca zmniejszając jednocześnie zmienną, która odpowiada za liczbę elementów kopca. Po zmniejszeniu tej liczby algorytm nie będzie "widział" tylnej, posortowanej już części tablicy.
Złożoność tego algorytmu to O(nlogn).

Sortowanie przez zliczanie (countingsort)

Sortowanie przez zliczanie ma jedną potężną zaletę i jedną równie potężną wadę:

• Zaleta: działa w czasie liniowym (jest szybki)
• Wada: może sortować wyłącznie liczby całkowite

Obydwie te cechy wynikają ze sposobu sortowania. Polega ono na liczeniu, ile razy dana liczba występuje w ciągu, który mamy posortować. Następnie wystarczy utworzyć nowy ciąg, korzystając z danych zebranych wcześniej. Np. mamy posortować ciąg: 3,6,3,2,7,1,7,1. Po zliczeniu (w jednym korku) operujemy danymi na temat liczności poszczególnych liczb:

• Liczba 1 występuje 2 razy
• Liczba 2 występuje 1 raz
• Liczba 3 występuje 2 razy
• Liczba 4 występuje 0 razy
• Liczba 5 występuje 0 razy
• Liczba 6 występuje 1 raz
• Liczba 7 występuje 2 razy

Na podstawie tych danych tworzymy ciąg: 1,1,2,3,3,6,7,7. Jest to ciąg wejściowy, ale posortowany. Należy zauważyć trzy ważne rzeczy:

1. Proces zliczania odbył się w jednym kroku
2. Nie doszło do ani jednej zamiany elementów
3. Proces tworzenia tablicy wynikowej odbył się w jednym kroku

Algorytmy ten posiada jednak również wady:

1. Do przechowywania liczby wyrazów ciągu musimy użyć tablicy, o liczbie elementów równej największemu elementowi ciągu
2. Sortować można jedynie liczby całkowite.

Sortowanie przez scalanie (mergesort)

Sortowanie przez scalanie (podobnie jak algorytm QuickSort, jest algorytmem typu "dziel i zwyciężaj". Jednak w odróżnieniu od QuickSort, algorytm ten w każdym przypadku osiąga złozoność T(n) = n*log(n). Niestety algorytm MergeSort posiada większą złożoność pamięciową, potrzebuje do swojego działania dodatkowej, pomocniczej struktury danych.
Ideą działania algorytmu jest dzielenie zbioru danych na mniejsze zbiory, aż do uzyskania n zbiorów jednoelementowych, które same z siebie są posortowane :), następnie zbiory te są łączone w coraz większe zbiory posortowane, aż do uzyskania jednego, posortowanego zbioru n-elementowego. Etap dzielenia nie jest skomplikowany, dzielenie następuje bez sprawdzania jakichkolwiek warunków. Dzięki temu, w przeciwieństwie do algorytmu QuickSort, następuje pełne rozwinięcie wszystkich gałęzi drzewa. Z kolei łączenie zbiorów posortowanych wymaga odpowiedniego wybierania poszczególnych elementów z łączonych zbiorów z uwzględnieniem faktu, że wielkość zbioru nie musi być równa (parzysta i nieparzysta ilość elementów), oraz tego, iż wybieranie elementów z poszczególnych zbiorów nie musi następować naprzemiennie, przez co jeden zbiór może osiągąć swój koniec wcześniej niż drugi. Robi sie to w następujący sposób. Kopiujemy zawartość zbioru głównego do struktury pomocniczej. Następnie, operując wyłącznie na kopii, ustawiamy wskaźniki na początki kolejnych zbiorów i porównujemy wskazywane wartości. Mniejszą wartość wpisujemy do zbioru głównego i przesuwamy odpowiedni wskaźnik o 1 i czynności powtarzamy, aż do momentu, gdy jeden ze wskaźników osiągnie koniec zbioru. Wówczam mamy do rozpatrzenia dwa przypadki, gdy zbiór 1 osiągnął koniec i gdy zbiór 2 osiągnął koniec. W przypadku pierwszym nie będzie problemu, elementy w zbiorze głównym są już posortowane i ułożone na właściwych miejscach. W przypadku drugim trzeba skopiować pozostałe elementy zbioru pierwszego pokolei na koniec. Po zakończeniu wszystkich operacji otrzmujemy posortowany zbiór główny.
Przykładowy przebieg algorytmu ukazany jest na schemacie poniżej: