<<wstecz   REKURENCJA

Charakterystyczną cechą funkcji (procedury) rekurencyjnej jest to, że wywołuje ona samą siebie. Drugą cechą rekursji jest jej dziedzina, którą mogą być tylko liczby naturalne. Najłatwiej zrozumieć mechanizm działania rekursji na przykładzie silni: rekurencyjny wzór na obliczenie n! zapisuje się w ten sposób: n!=n*(n-1)!, przy czym 0! oraz 1! = 1.
Ze wzoru tego wynika, że aby obliczyć np. 4!, należy najpierw obliczyć 3!. Ale żeby obliczyć 3! trzeba obliczyć 2! itd. aż dojdziemy do 0!, które jak wiemy wynosi 1.
Sposób obliczenia 4! wygląda więc następująco:
4!=4*3!=4*3*2!=4*3*2*1!=4*3*2*1*0!=4*3*2*1*1=24

Ia. Rekurencyjna wersja silni

W przykładzie tym została zastosowana procedura (tworzenie procedur).

Można zbudować algorytm, który będzie składał się z kilku plansz, zawierających procedury. Procedura musi zaczynać się od klocka Początek Procedury, a kończyć na klocku - Koniec Procedury. Może być ona budowana na tej samej planszy co główny algorytm, ale lepiej, by każda procedura miała osobną planszę. Aby procedura była funkcją (zwracała wartość), w klocku wywołującym procedurę w algorytmie nadrzędnym trzeba wypełnić pole: Nazwa zmiennej - wstawiając nazwę zmiennej, której przypisana zostanie wartość zwracana przez procedurę, a w klocku kończącym procedurę wpisać wyrażenie, którego wartość będzie zwracana.
Posługiwanie się procedurami jest wygodne z paru powodów. Po pierwsze skraca to algorytmy tak, że nie rozrastają się poza ekran. Łatwiejszy staje się proces poprawiania błędów. Po drugie zdarza się, iż podobny ciąg kroków jest wykonywany w różnych miejscach algorytmu. Ujęcie go w procedurę daje dużą oszczędność - wpisujemy go tylko raz, a potem wywołujemy jednym klockiem. Wreszcie, z procedur można stworzyć bibliotekę rozwiązanych problemów - tą samą procedurę może wykorzystywać wiele algorytmów.
Wartości zmiennych nie są automatycznie przenoszone do procedur. Dzieje się tak tylko wtedy, gdy zmienne zadeklarujemy jako globalne. Żeby to zrobić należy na jednej z plansz projektu umieścić klocek deklaracji zmiennych globalnych z wpisanymi nazwami zmiennych.
Plansza głównego algorytmu i plansze procedur tworzą projekt. Jest on zapisywany na dysku (Plik/Zachowaj projekt) w postaci pliku opisującego konfigurację o rozszerzeniu .PRJ. Oprócz tego powinny być zapisane wszystkie plansze składające się na projekt (Plik/ Plansza/Zachowaj). Pełna informacja tym z jakich plansz składa się projekt jest zawarta w oknie projektu.

W zestawie podstawowych klocków znajdują się 4 klocki obsługujące procedury:

Wywołanie procedury - przekazanie sterowania do procedury.
Początek procedury - rozpoczyna wykonanie procedury
Koniec procedury - kończy wykonanie procedury i powoduje powrót do planszy, z której został wywołany.
Deklaracja zmiennych globalnych, czyli wspólnych dla różnych plansz projektu.

1 start (program główny) obliczanie silni dla wartości 0-10 2 silnia:=1 liczba:=1 ustawienie wartości początkowych 3 zapis do tablicy wypisanie silni dla wartości 0 w tablicy kolumna <0>, wiersz <0>, wyrażenie <silnia> 4 wywołanie procedury nazwa <silnia>, paramerty <liczba, silnia> 5 koniec     1 utworzenie procedury nazwa <silnia>, parametry <liczba, silnia> 2 silnia:=silnia*liczba przypisanie silni wartości iloczynu liczby i silni 3 zapis do tablicy wypisanie silni do tablicy w kolumnie <0> i wierszu <liczba>, wyrażenie <silnia> 4 liczba:=liczba+1 przypisanie liczbie wartości wiekszej o 1 5 warunek - czy liczba jest większa od 10? jeśli TAK, zakończenie procedury (powrót do programu głównego) 6 jeśli NIE, wywołanie procedury (ponowne wywołanie procedury)

Ib. Iteracyjna wersja silni

1 start   2 wczytaj n wczytaj wartość silni 3 licznik:=0 silnia:=1  ustawienie wartości początkowych 4 czy licznik = n jeśli TAK idź do kroku 6 5 licznik:=licznik+1 silnia:=silnia*licznik idź do kroku 4 zwiększenie licznika o 1 obliczanie kolejnego współczynnika silni 6 wypisz <silnia>   7 koniec

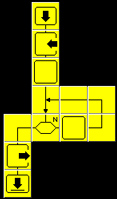II. Ciąg Fibonacciego.

Ciąg Fibonacciego ma następującą konstrukcję: pierwsze dwa wyrazy to jedynki, każdy następny wyraz powstaje przez dodanie dwóch bezpośrednio go poprzedzających.

F(1) = 1; F(2) = 1; F(n) = F(n-1) + F(n-2).

Spróbujcie sami wypisać 10 kolejnych wyrazów ciągu: najpierw jedynka, pod nią druga, dodajemy i pod spodem dopisujemy wynik, dodajemy dwa ostatnie wyrazy, wypisujemy wynik...

Zapiszmy ten schemat obliczeń, używając taśmy do zapamiętywania kolejnych wyrazów. Niech numer pozycji na taśmie będzie numerem wyrazu ciągu.

1 start   2 wczytaj n wczytanie liczby wyrazów ciągu n 3 taśma przesunięcie taśmy na pozycję 1 4 taśma zapisanie na taśmie jedynki (pierwszy wyraz) 5 sprawdzenie czy n=1 jeśli TAK, to idź do kroku 15 6 taśma jeśli NIE to zapisanie na taśmie jedynki (drugi wyraz) 7 i:=3   8 sprawdzenie czy i > n jeśli TAK to idź do kroku 15 9 jeśli NIE to   10 taśma przesuń wskaźnik na pozycję i - 2 11 taśma przypisanie zmiennej <f1> odczytanej z taśmy wartości 12 taśma przypisanie zmiennej <f2> odczytanej z taśmy wartości 13 taśma zapisanie na taśmie wartości <f1 + f2> 14 i:=i + 1 powrót do kroku 8 wykonanie obliczenia   15 koniec