<<wstecz ITERACJA
ITERACJA (działanie w pętli) to technika algorytmiczna polegająca na wykonaniu tej samej instrukcji dla n zmiennych (np. liczb, wartości logicznych etc.) Iteracja oszczędza czas programisty, który ten musiałby spędzić wpisując instrukcję n razy, zależnie od liczby zmiennych. Liczba powtórzeń w iteracji jest z góry określona lub zależy od spełnienia określonego warunku (FOR, WHILE).
Przykłady:
I. Suma i średnia n liczb ciągu 1 2 3 4 5 ... n
zauważamy, że kolejne wyrazy mają postać
1 i=1 1
2 i=2 2 itd czyli i
|
 |
(oczywiście można nie obliczać wyrazu i krok 6 przedstawić tak --> suma:=suma + i ,
a można inaczej ... (jak prawdopodobnie zrobił młody Gauss - gdy jeszcze był uczniem) ale trzeba zauważyć, że to suma ciągu arytmetycznego która wynosi n*(n+1)/2
Mamy więc:
1 |
start |
|
2 |
wczytaj n |
czyli ilości wyrazów do pomnożenia |
3 |
wypisz n*(n+1)/2 |
suma |
4 |
koniec |
II. Suma i średnia nieznanej ilości liczb.
|
 |
III. Największy wspólny dzielnik NWD liczb a i b (algorytm Euklidesa).
|
 |
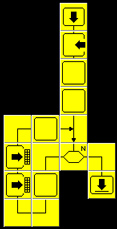
IV. Sumowanie liczb nieparzystych (w tablicy)
Tablica służy do przechowywania danych i ma budowę podobną do tabeli - składa się z wierszy i kolumn. Element tablicy można znaleźć znając numer jego wiersza i kolumny - czyli adres w tablicy. Wiersze i kolumny są ponumerowane od zera. W pierwszym, nie ponumerowanym wierszu można umieścić opis - dowolny napis. Do każdego pola można wstawić wartość - należy w tym celu wskazać kursorem myszki to pole, nacisnąć klawisz Shift i lewy przycisk myszy i wpisać liczbę. Po naciśnięciu Enter w wybranym polu pojawi się wpisana wartość. Klocek Zapis do tablicy użyty w algorytmie powoduje ten sam efekt, natomiast klocek Odczyt z tablicy powoduje pobranie wartości z podanego pola tablicy.
![]() Odczytaj z tablicy
Odczytaj z tablicy
![]() Zapisz do tablicy
Zapisz do tablicy
Zapisywanie wyników w tablicy pozwoli na oglądanie kolejnych sum. W kolumnie 0 będziemy zapisywać kolejne liczby nieparzyste (i), a w kolumnie 1 - sumy.
|
 |
V. Przeliczanie liczby z układu dziesiętnego na dwójkowy.
|
 |
VI. Przeliczamy z układu dwójkowego na dziesiętny
Algorytm ten ma działanie odwrotne od poprzedniego. Do algorytmu będzie wprowadzana liczba w systemie dwójkowym, czyli ciąg cyfr 0 i 1. W wyniku powinniśmy otrzymać liczbę całkowitą w układzie dziesiętnym. Wzór na przeliczanie wygląda następująco - LiczbaDziesiętna := w0*2^0 + w1*2^1 + ... + wn*2^n. Musimy zdecydować w jaki sposób będziemy wczytywać współczynniki. Powiedzmy, że zostaną one odczytane z taśmy, tak że skrajna prawa cyfra - współczynnik przy potędze 0 będzie na początku (na pozycji 0, wtedy numer pozycji na taśmie będzie odpowiadał potędze dwójki). Na końcu algorytmu powinien zostać wypisany wynik w postaci liczby dziesiętnej. (Aby algorytm działał poprawnie musimy mieć otwartą taśmę z dowolną liczbą w systemie dwójkowym.)
|
 |
VII. Szukamy wylosowanej liczby
Zbudujemy algorytm realizujący zabawę w zgadywanie liczby.
Wybierzmy zakres: od 0 do 100, komputer losuje liczbę z tego zakresu (trzeba użyć funkcji losowa(n) zwracającej pseudolosową liczbę z przedziału 0 - n-1), a my ją mamy odgadnąć, otrzymując tylko informacje, czy podana liczba jest za mała, czy też za duża. Po wczytaniu naszej liczby algorytm ma więc do wyboru trzy możliwości: 1 - trafiona, 2 - za mała, 3 - za duża.
Interesuje nas nie tylko budowa algorytmu ale także wyniki jego działania. Podawane przez nas liczby są zapisywane na taśmie. Po trafieniu możemy więc prześledzić historię gry. Czy udaje się Wam zgadnąć liczbę w najwyżej siedmiu krokach? Jeśli nie, to powinniście popracować nad strategią zgadywania.
Najlepsza strategia zgadywania liczby - to metoda połowienia nazywana także przeszukiwaniem binarnym.
|
 |